Research articles
ScienceAsia (): 279-284 |doi:
10.2306/scienceasia1513-1874...279
Multiple solutions for k-coupled Schrödinger system with variable coefficients
Xin Wang, Lijie Yin, Xiaorui Yue*
ABSTRACT: Consider the k-coupled Schrödinger system with variable coefficients as below which arises in nonlinear
optics and other physical problems:
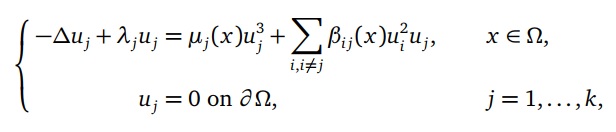
where Ω is a bounded smooth domain in R
N
, N ≤ 3, k≥ 2; λj > −λ1
(Ω) for j = 1, . . . , k and λ1
(Ω) is the first eigenvalue
of −∆ with Dirichlet boundary condition; µj
(x) and βi j(x) = βji(x) are positive bounded functions for i, j ≠, . . . , k,
i 6= j. We obtain multiple solutions with some components sign-changing while the others positive, and one positive
solution for the above problem.
Download PDF
69 Downloads 1746 Views
| a |
College of Information Science and Technology, Hainan University, Haikou, Hainan 570228, China |
* Corresponding author, E-mail: yxr@hainu.edu.cn
Received 8 Oct 2018, Accepted 28 May 2019
|