Research articles
ScienceAsia (): 388-394 |doi:
10.2306/scienceasia1513-1874...388
A note on differential-difference analogue of Brück
conjecture
Minfeng Chena,*, Ning Cuib
ABSTRACT: In this paper, we prove that for a transcendental entire function ƒ (z) of finite order, η ∈ C\\{0} is a constant
such that ∆
η ƒ (z) = ƒ (z+η)− ƒ (z) ≢0, b(z) is an entire function such that σ(b) < σ(ƒ ) and λ(ƒ −b) < σ(ƒ ), if ∆η ƒ (z)
and ƒ 0(z) share a(z) CM, where a(z) is an entire function satisfying σ(a) < σ(ƒ ), then
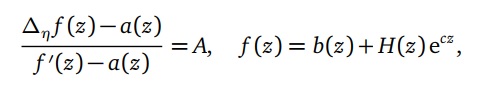where a(z) and b(z) are entire functions with max{σ(a),σ(b)} < 1, H(z)(≢ 0) is an entire function with λ(H) =
σ(H) < 1 and A, c,η ∈ C\\{0} are constants satisfying ecη = 1 + Ac. Our results are improvements and complements of
those in [Bull Korean Math Soc 51 (2014) 1453-1467] and [Commun Korean Math Soc 32 (2017) 361-373].
Download PDF
55 Downloads 1552 Views
| a |
School of Mathematics and Statistics, Guangdong University of Foreign Studies, Guangzhou 510006,
China |
| b |
College of Mathematics and Information Science, Zhengzhou University of Light Industry, Zhengzhou
450002, China |
* Corresponding author, E-mail: chenminfeng198710@126.com
Received 1 Mar 2019, Accepted 0 0000
|
